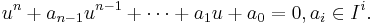Integral element
In commutative algebra, an element b of a commutative ring B is said to be integral over its subring A if there are 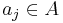 such that
such that
That is to say, b is a root of a monic polynomial over A.[1] If B consists of elements that are integral over A, then B is said to be integral over A or B is an integral extension of A.
If A, B are fields, then the notions of "integral over" and of an "integral extension" are precisely "algebraic over" and "algebraic extensions" in field theory (since one does not have to insist on "monic".) The special case of greatest interest in number theory is that of complex numbers integral over Z; in this context, they are usually called algebraic integers (e.g., 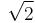 .) A ring consists of some (not all) algebraic integers is called the ring of integers, a central object in algebraic number theory.
.) A ring consists of some (not all) algebraic integers is called the ring of integers, a central object in algebraic number theory.
In this article, the term ring will be understood to mean commutative ring with a unity.
Contents |
Examples
- Integers are the only elements of Q that are integral over Z (Thus, Z is the integral closure of Z in Q.)
- Gaussian integers, complex numbers of the form
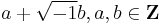 , are integral over Z. (cf. quadratic integers.)
, are integral over Z. (cf. quadratic integers.) ![\mathbf{Z}[\sqrt{-1}]](/2012-wikipedia_en_all_nopic_01_2012/I/aea83b47e1673ba8d4697693a77b6b7d.png) is then the integral closure of Z in
is then the integral closure of Z in ![\mathbf{Q}[\sqrt{-1}]](/2012-wikipedia_en_all_nopic_01_2012/I/da28f08f03a1b3d45b31262c6fa6c04d.png) .
. - The roots of unity and nilpotent elements are integral over Z.
- The integral closure of Z in the field of complex numbers C is called the ring of algebraic integers.
- Let a finite group G act on a ring A. Then A is integral over
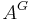 the set of elements fixed by G.
the set of elements fixed by G. - Let R be a ring and u a unit in a ring containing R. Then (i)
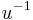 is integral over
is integral over  if and only if
if and only if ![u^{-1} \in R[u].](/2012-wikipedia_en_all_nopic_01_2012/I/da3f3e15f270ca28076db6f7e41c7b84.png) (ii)
(ii) ![R[u] \cap R[u^{-1}]](/2012-wikipedia_en_all_nopic_01_2012/I/c43cf678816f4e2a9a243ff09a081bf1.png) is integral over R.[2]
is integral over R.[2]
Equivalent definitions
Let B be a ring, and let A be a subring of B. Given an element b in B, the following conditions are equivalent:
-
- (i) b is integral over A;
- (ii) the subring A[b] of B generated by A and b is a finitely generated A-module;
- (iii) there exists a subring C of B containing A[b] and which is a finitely-generated A-module;
- (iv) there exists a finitely generated A-submodule M of B with
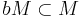 and the annihilator of M in B is zero.
and the annihilator of M in B is zero.
The usual proof of this uses a variant of Cayley–Hamilton theorem on determinants (or simply Cramer's rule.) Specifically, one can use (Matsumura):
- Theorem Let u be an endmorphism of an A-module M generated by n elements and I an ideal of A such that
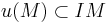 . Then there is a relation:
. Then there is a relation:
This theorem (with I = A and u multiplication by b) gives (iv) 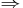 (i) and the rest is easy. (Note the generality on an ideal I is useful for the consideration of the integral closure of an ideal.) Coincidentally, Nakayama's lemma is also an immediate consequence of this theorem.
(i) and the rest is easy. (Note the generality on an ideal I is useful for the consideration of the integral closure of an ideal.) Coincidentally, Nakayama's lemma is also an immediate consequence of this theorem.
It follows from the above that the set of 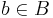 that is integral over A forms a subring of B containing A. It is called the integral closure of A in B. The proof is due to Dedekind (Milne, ANT). Alternatively, one can use symmetric polynomials to show integral elements form a ring. (loc cit.) If A happens to be the integral closure of A, then A is said to be integrally closed in B. If A is reduced (e.g., a domain) and B its total ring of fractions, one often drops qualification "in B" and simply says "integral closure" and "integrally closed."[3]
that is integral over A forms a subring of B containing A. It is called the integral closure of A in B. The proof is due to Dedekind (Milne, ANT). Alternatively, one can use symmetric polynomials to show integral elements form a ring. (loc cit.) If A happens to be the integral closure of A, then A is said to be integrally closed in B. If A is reduced (e.g., a domain) and B its total ring of fractions, one often drops qualification "in B" and simply says "integral closure" and "integrally closed."[3]
Similarly, "integrality" is transitive. Let C be a ring containing B and c in C. If c is integral over B and B integral over A, then c is integral over A. In particular, if C is itself integral over B and B is integral over A, then C is also integral over A.
If A is noetherian, one has a simpler criterion for integrality: b is integral over A if and only if there is a nonzero d such that 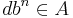 for all
for all 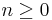 . This can be used to weaken (iii) in the above to
. This can be used to weaken (iii) in the above to
- (iii) bis There exists a finitely generated A-submodule of B that contains
![A[b]](/2012-wikipedia_en_all_nopic_01_2012/I/4ac85d626c6f04e66c0373ad479130df.png) .
.
Finally, the assumption that A be a subring of B can be modified a bit. If f: A 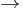 B is a ring homomorphism, then one says f is integral if
B is a ring homomorphism, then one says f is integral if 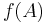 is integral over B, in the same way one says f is finite (B finitely generated A-module) or of finite type (B finitely generated A-algebra). In this view point, one can says
is integral over B, in the same way one says f is finite (B finitely generated A-module) or of finite type (B finitely generated A-algebra). In this view point, one can says
- f is finite if and only if f is integral and of finite-type.
Or, more explicitly,
- B is a finitely generated A-module if and only if B is generated as A-algebra by a finite number of elements integral over A.
Integral extensions
One of the Cohen-Seidenberg theorems shows that there is a close relationship between the prime ideals of A and the prime ideals of B. Specifically, they show that an integral extension A⊆B has the going-up property, the lying over property, and the incomparability property. In particular, the Krull dimension of A and B are the same.
When A, B are domains, A is a field if and only if B is a field.
Let 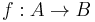 be an integral extension of rings. Then the induced map
be an integral extension of rings. Then the induced map 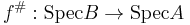 is closed. This is a geometric interpretation of the going-up property.
is closed. This is a geometric interpretation of the going-up property.
Integral closure
Let 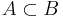 be rings and A' the integral closure of A in B. (See above for the definition.)
be rings and A' the integral closure of A in B. (See above for the definition.)
Integral closures behave nicely under various construction. Specifically, the localization S−1A' is the integral closure of S−1A in S−1B, and ![A'[t]](/2012-wikipedia_en_all_nopic_01_2012/I/fb66b632d9c6bd3de2fcb99acecba884.png) is the integral closure of
is the integral closure of ![A[t]](/2012-wikipedia_en_all_nopic_01_2012/I/cdeb6c184a89fa8999faa214d8ef08ea.png) in
in ![B[t]](/2012-wikipedia_en_all_nopic_01_2012/I/240be3b61f4a2fd8112c881bced19f8c.png) .[4]
.[4]
The integral closure of a local ring A in, say, B, need not be local. This is the case for example when A is Henselian and B is a field extension of the field of fractions of A.
If A is a subring of a field K (A is necessarily a domain), then the integral closure of A in K is the intersection of all valuation rings of K containing A.
Assume A is reduced. The conductor of A is 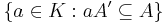 : it is the largest ideal of A that is also an ideal of
: it is the largest ideal of A that is also an ideal of 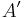 .[5] If the conductor is A, then A is integrally closed. Note this is a generalization of the same concept in algebraic number theory.
.[5] If the conductor is A, then A is integrally closed. Note this is a generalization of the same concept in algebraic number theory.
There is a concept of the integral closure of an ideal. The integral closure of an ideal 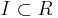 , usually denoted by
, usually denoted by 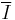 , is the set of all elements
, is the set of all elements 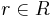 such that there exists a monic polynomial
such that there exists a monic polynomial  with
with 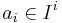 with
with  as a root. The integral closure of an ideal is easily seen to be in the radical of this ideal.
as a root. The integral closure of an ideal is easily seen to be in the radical of this ideal.
There are alternate definitions as well.
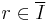 if there exists a
if there exists a 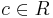 not contained in any minimal prime, such that
not contained in any minimal prime, such that 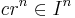 for all sufficiently large
for all sufficiently large  .
.
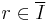 if in the normalized blow-up of
if in the normalized blow-up of  , the pull back of
, the pull back of  is contained in the inverse image of
is contained in the inverse image of  . The blow-up of an ideal is an operation of schemes which replaces the given ideal with a principal ideal. The normalization of a scheme is simply the scheme corresponding to the integral closure of all of its rings.
. The blow-up of an ideal is an operation of schemes which replaces the given ideal with a principal ideal. The normalization of a scheme is simply the scheme corresponding to the integral closure of all of its rings.
The notion of integral closure of an ideal is used in some proofs of the going-down theorem.
Noether's normalization lemma
Noether's normalisation lemma is a theorem in commutative algebra. Given a field K and a finitely generated K-algebra A, the theorem says it is possible to find elements y1, y2, ..., ym in A that are algebraically independent over K such that A is finite (and hence integral) over B = K[y1,..., ym]. Thus the extension K ⊂ A can be written as a composite K ⊂ B ⊂ A where K ⊂ B is a purely transcendental extension and B ⊂ A is finite.[6]
Notes
- ^ The above equation is sometimes called an integral equation and b is said to be integrally dependent on A (as opposed to algebraic dependent.)
- ^ Kaplansky, 1.2. Exercise 4.
- ^ Chapter 2 of Huneke and Swanson 2006
- ^ An exercise in Atiyah–MacDonald.
- ^ Chapter 12 of Huneke and Swanson 2006
- ^ Chapter 4 of Reid.
References
- M. Atiyah, I.G. Macdonald, Introduction to Commutative Algebra, Addison–Wesley, 1994. ISBN 0201407515
- Kaplansky, Irving (September 1974). Commutative Rings. Lectures in Mathematics. University of Chicago Press. ISBN 0226424545.
- H. Matsumura Commutative ring theory. Translated from the Japanese by M. Reid. Second edition. Cambridge Studies in Advanced Mathematics, 8.
- J. S. Milne, "Algebraic number theory." available at http://www.jmilne.org/math/
- Huneke, Craig; Swanson, Irena (2006), Integral closure of ideals, rings, and modules, London Mathematical Society Lecture Note Series, 336, Cambridge, UK: Cambridge University Press, ISBN 978-0-521-68860-4, MR2266432, http://people.reed.edu/~iswanson/book/index.html
- M. Reid, Undergraduate Commutative Algebra, London Mathematical Society, 29, Cambridge University Press, 1995.